Introduction
This article is a non-mathematical description of the dynamic economic modeling methods developed by Steve Keen.
In a number of papers and articles Steve Keen describes a mathematical model of the economy built using dynamic modeling techniques. The details of each model vary depending on the title and purpose of the article, but there is a very easily identified core set of components, relationships and methods which can sensibly be described as Steven Keen’s Dynamic Monetary Economic model. I am going to try to give a non-mathematical overview of these core ideas so that anyone who wants to go and read those papers, but does not have much mathematical preparation, can get as much from them as possible.
The use of continuous dynamic modeling is a key feature of Steve’s economic model and a general understanding (albeit non mathematical) of dynamic modeling is necessary to understand it. There are therefore three parts to this article. Firstly a non-mathematical introduction to continuous dynamic modeling in general; secondly a non-mathematical description of the Steve’s dynamic model itself; and lastly a discussion of the graphs which the model creates and which you will see in Steve’s papers.
Part 1. Continuous Dynamic Modeling
A dynamic model describes the behaviour of a system over time. It consist primarily of a number of variables (about 10 in Steve’s case) each having its own modeling formula to control its evolution over the time period being modeled/simulated.
Crucially, and slightly confusingly, in a dynamic model the modeling formulae are not used to ‘set’ the value of their related variable directly but instead are used to change it. After the modeling variables are given an initial value at the beginning of the simulation they continually change at a rate (and direction) determined moment to moment by their controlling formula which take as their inputs the states of some or all the variables in the model including the one it is responsible for.
This focus on change (rather than state) is very significant and is what makes dynamic models so useful for economics because it allows the variables to move much more freely relative to each other so they can do things like cycle and crash.
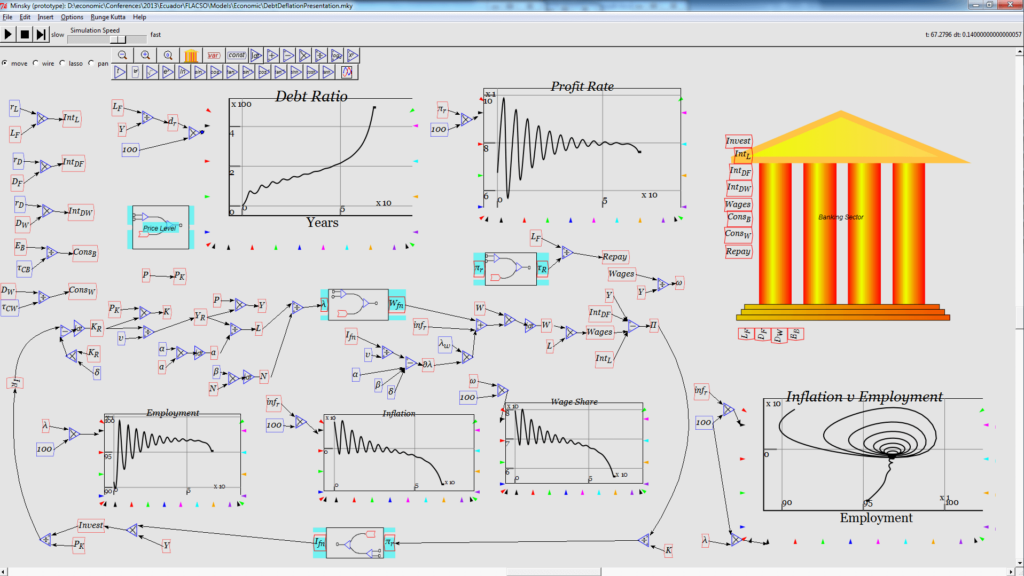
Although the modeling technique is called ‘Continuous’, computers can only deal in discrete steps. In each tiny step the value of each variable is calculated from its previous value plus the change generated by its modeling formula. The values of each variable at each step are recorded in a table and form the output of the model which can be viewed on line graphs.
Time slicing like this is only an approximation of continuous reality and incurs errors which build up over time. The approximation, however, can be made as accurate as any particular application requires by altering the size of the time steps and the precision of the maths engine used. This ‘approximation’ process was used, in fact, to plot the course of the astronauts to the moon and is still used today for all space navigation involving more than 2 masses.
An important reason that the complexities of dynamic modeling are tolerated is that they can reproduce the cyclic and catastrophic behaviour we see in the economy (and other complex dynamic systems) whereas the static modeling methods used by traditional economists cannot.
At the time traditional economics was developed computers were not around. Economics was forced to develop using static models where external shocks were the only way cyclical and catastrophic events could be explained. After the 1930s depression it was noticed by some that the economy behaved like a dynamic system but the computers were not around to support those theories and so they faded away… until 2007 when it all happened again. And this time we do have computers…
Part 2. Steve Keen’s Dynamic Monetary Model of the Economy
Steve’s models are comprised of two distinct groups of variables: The ‘Financial’ variables and the ‘Production’ variables. The production variables (and their formulae) model economic statistics like wage level, quantities and Price Level. The Financial variables (and their formulae) model money/debt flows in and out of small number of notional banking sector ‘accounts’.
Here are the 5 financial (bank) sector account variables which you will find in most of Steve’s Dynamic Monetary Models : –
Bank Vault. – Representing the banking sector’s monetary assets;
Bank Transactions Account – into which interest from customers is paid and from which bank expenditure are made.
Firm Loan ledger – which is not an account that can store money but a record of the amount of outstanding debt owed by the firm sector to the banking sector
Firm Deposit Account – into which money borrowed by the firm sector is deposited
Household Deposit Account – into which wages are paid.
And here are the 3 ‘production’ variables.
- Capital Stock
- Price Level
- Wage Rate
The modeling formulae for these variables are created by considering a number of real world operations. Here is the list of operations used in Steve’s XYZ paper.
- Lending of money from the bank vault to the firms’ deposit accounts.
- Payment of interest by firms to the bank’s transactions account.
- Payment of interest by the bank on firms’ deposit accounts.
- Payment of wages.
- Payment of interest on workers’ account balances.
- Payment for consumption of the output of firms by bank and workers.
- Repayment of loans by firms.
- Recording the loans of the existing money stock to firms.
- Compounding the debt at the rate of interest on loans.
- Recording the payment of interest on loans.
- Recording the repayment of loans.
- Recording the endogenous creation of new money.
- The endogenous creation of new money in response to firms’ investment plans.
Notice there is no relationship between the number of operations and the number of modeling variables. The way these operations are analyzed to create the modeling formulae (one for each variable) is central to Steve’s whole modeling method.
Just as in the real world the ‘books’ of the financial sector must always balance; credits must equal debits etc. To ensure this balance the modeling formulae for the financial variables are derived in the same way that an accountant works:
First the size of each operation is calculated (the amount of money involved). The simplest example of this in Steve’s model is the payment of interest, by the bank, on firms’ deposit accounts. (operation 3 above) The ‘size’ of this operation is simply the rate of deposit interest times the amount of money in the ‘Firm Deposit’ account (fourth item in the list of variables above)
After determining the size of the operation we identify which variables are affected by the operation. In our example, paying interest on firm’s deposits reduces the size of the Bank Transaction account and simultaneously increases the size of the Firm Deposit account by the same amount. This means that the interest calculation appears with a minus sign in the formula controlling the Bank Transaction account and with a plus sign in the formula controlling the Firm Deposit account. It should be apparent that the net result of the operation does not change the amount of money in circulation; it just moves funds around and so accounting integrity has been maintained.
Note that some operations actually do increase the amount of money in circulation (i.e. endogenous money creation) but accounting integrity is still maintained by matching deposits with loan obligations (Firm Loans with Firm Deposits).
This same process is repeated for every operation in the list, gradually building the modeling formula for the financial variables. Because each separate operation is financially credible it can be assumed that the resultant final modeling formula, which are just the sum of all those operations, are also financially credible.
The process by which the controlling formula for the production variables are derived is more arbitrary. Each formula is justified using a separate economic theories; either Steve’s own or other people’s.
Just to give you flavor of what sort of thing we are talking about here is direct quote from the section of the paper dealing with the derivation of the formula controlling the Wage variable
“ … The dynamic disequilibrium price equation is consistent with empirical research into actual price setting behavior (Blinder, 1998; Lee,1998) and is derived analytically in (Keen, 2010) from the equilibrium condition for physical output and the physical demand for commodities. Prices converge to a mark-up over the monetary cost of production, where the mark up factor (1−) is equivalent to the equilibrium workers’ share of real output...”
You should be able to see that this is descriptive economic theory being used to generate a mathematical formula to control a variable in the model.
The last thing to note is that Financial and Production variables interact via their controlling formula which access all variables not just ones in their own category. For instance the size of the wage payments operation (number 4 in the list above) references the Wage Rate variable whose controlling formula was being developed in the direct quote from Steve’s paper above.
And that’s it. We have a set of variables and a formula for each to control how it changes over time. To run the model we simply….
1) Enter the variables and formulae into a Dynamic Modelling package – such as Steve’s own ‘Minsky’
2) Select starting values for the variables (normally set to something other than just zero)
3) Hit the ‘Start Simulation’ button.
Part 3. Graphic output of Steve’s Models
The output of a dynamic model consists of a time series for each of the variables in the model. I.e. a list of values for each variable sampled at regular intervals over the period of the simulation.
It is possible to view this output on a line graph where the X axis represents time, the Y axis represents Money (usually) and each variable has a line displaying its value changing over time. Here is a time series line graph showing the Bank Vault, Firm Loan and Firm Deposit variables from a run of the model. Initially all three variables rise at pretty much the same rate until at about year 50 in the simulation Firm Loans and Deposits collapse whilst the Bank Vault jumps up. This behaviour is exactly what we saw in the great recession. Loans deposits go down as firm investment goes down which causes bank reserves to go up.
As well as simply graphing the model variables we can graph values which are calculated from the variables in the model. Here is a graph of the percentage of GDP earned by Workers, Capitalists and Bankers receive. These are not directly modeled but can be easily calculated from the variables which are in the model.

This chart nicely shows the ‘Great Moderation’ as a series of gradually smaller cycles in GDP share until at around year 50 of the simulation, just as the system seems to settle down, the whole pattern of distribution radically changes: Capitalists and workers both lose share and bankers (ironically) gain it.
Phase Diagrams
Dynamic model output is also commonly viewed as something called a phase diagram which is line graph where each axis represents a single variable from the model. The results are shown as a single line on the graph. The coordinates of each point on the line represent the values of the axis variables at one particular instant.
Here is a fancy looking 3 dimensional phase diagram from one of Steve’s models constructed along the lines described above.
To interpret phase diagrams you have to imagine a dot traveling along the line. It would not be wrong to mark the direction of travel on the line with an arrow although it is normally assumed that this is obvious to an informed viewer. As time progresses the dot moves along the line and its co-ordinates change representing the changing values of the variables they represent. In this case the direction of movement (time) is from the dark purple end of the line at the bottom to the red end at the top.
The circling/spiraling section of the path at the bottom is at the start of the period being modeled. In this early period both ‘debt to output ratio’ and ‘Employment’ go up and down but out sync with each other producing the circling pattern (this is a common pattern in nonlinear dynamic models) During this cyclic phase debt remains low as a proportion of output, but once again at the end of the run it gets out of control and heads upwards rapidly as output collapses.
Conclusions
Clearly this is only the briefest of introductions to Steve’s dynamic models. The key point is that dynamic modeling can reproduce the behaviours we see in the real world as an emergent result whose individual components can each be justified in intuitively satisfying ways relating to day-to-day activities having nothing to do with these emergent results.
More to read:
Key Benefits of Hiring Experienced Commercial Lawyers in Sydney
How Commercial Lawyers Help Your Business Navigate Legal Challenges



